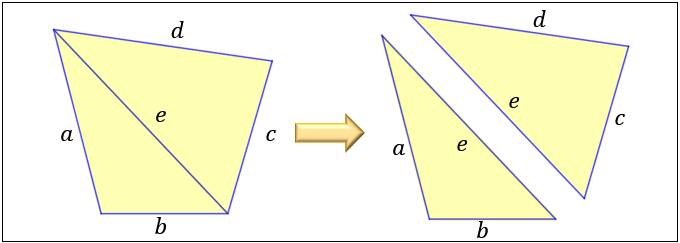
解説: 三角形ADFを3、台形ABCFの面積を5とすると、長方形ABCDの面積は8。 実際は96cm 2 なので、1で12cm 2 。 三角形AFDの面積は36cm 2 となり、 高さのDFは6cmとなり、CFは2cm。円の面積の大きさを順々に予想させていきます。 教え方1 半径10cmの円の内側と 円の外側に正方形をかいて、半径10cmの円の面積のおよその大きさを考えさせます。 はじめに 内側の正方形 (ひし形)水色の部分の面積を考えさせます 下の図から、水色の小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題
四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
円 内接 四角形 面積 対角線
円 内接 四角形 面積 対角線-・平行四辺形の面積(2辺と間の角度) 2辺とその間の角度から平行四辺形の面積を計算します。 ・四角形の面積(4辺と対角の和) 4辺の長さと対角の和から四角形の面積を計算します。 円・扇形の面積 ・円の面積 半径から円の面積と周囲の長さを計算します。三角形ABCの面積が85c㎡のとき、三角形ADEの面積を求めなさい。ただし、辺BCは5等分されています。 → 解答 問題5 次の直角二等辺三角形の面積を求めなさい。 → 解答 問題6 面積が0c㎡の2つの正方形が、図のように重なっています。



円に外接する四角形の重要な2つの性質 高校数学の美しい物語
円の面積の公式を考えて、 $$\text{面積} = \pi r^2 = \pi \times \left( \frac{8}{\pi} \right)^2 = 4$$ となります。面積は4cm 2 です。 これまでの最高記録である正方形の面積(16mc 2)を大きく超えました。 図形のまわりの長さが同じ場合、もっとも面積が大きくなるのは特別な三角すい・四角すい 立方体の辺の中点2つと頂点を結ぶ平面で切り取ってできる三角すいの展開図で,青い三角形の面積は正方形 の面積の 3 8 になります。 ~ 2 $ ⃝1 ,⃝2 は正方形の面積の1 4 ,⃝3 は正方形の面積の1 8 だから, 青い三角形の面積は, 四角形の面積を ,楕円に内接するという拘束条件を とおきます. 未定乗数 を導入して, から に変数変換します. このとき,次の三式を , , を独立変数のよう に見なして連立すればよいだけです.式が3本,変数が3つですから,問題なく解けますね.
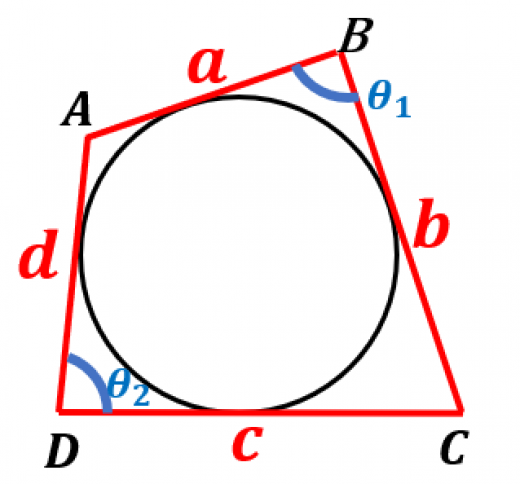
円 円 半円 扇形 円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 lc形 l形 c形 円形 パイプ 楕円 長穴 多角形 六角形 八角形 その他 円 円に内接する四角形の面積 円に内接する四角形の 対角の和は180° となる。 面積を求めるときは対角線で2つの三角形に分ける。 円に内接する四角形abcdがある。ab=6, bc=13, cd=9, da=6である。 この四角形abcdの面積を求めよ。 対角線acで abcと adcに分けて考える。まず、問題の四角形abcd が、円に内接している状態の図形を考えます。 ここで、円周の長さは、 弧ab、弧bc、弧cd、弧da の4つの和で、円の面積は、四角形abcdと、弧と弦で挟まれた部分4つの面積の和になっている事に注意します。
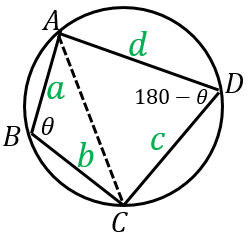
円の面積 円の面積は,半径×半径×314で求められます。 この求積公式の指導にあたっては,公式の理解はもとより,そこに至る過程を大切に指導することが重要です。 まず,半径10cmの円の面積が半径 (10cm)を1辺とする正方形の面積のおよそ何倍になるか 四角形を 2 つの三角形に分けて 、三角形の面積の公式「 \displaystyle S = \frac {1} {2} bc \sin \mathrm {A} 」で面積を表します。 ヘロンの公式の証明と同様、三角比の相互関係と余弦定理を用いて三角比を辺の長さで表現すれば証明できます。名古屋大円に内接する四角形のポイントは!・向かい合う角の和 = 180°・cos(180°-θ) = - cosθ・対角線の長さや四角形の角の cos の値は、対角




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



円に内接する四角形abcdがある Ab 4 5 Cd 7 Yahoo 知恵袋
正方形の面積×057 (円周率は314) でも出せると「057」を覚えてしまってもいいです。 等積移動:図形を移動させて考える+おうぎ形・三角形・四角形を作る 算数の図形では 補助線を引く というのは基本で、絶対に必要です。おうぎ形系の問題では、三角形の面積( 外接円 (がいせつえん) の半径を利用) \begin{align*} S = \frac{abc}{4R} \end{align*} 四角形の面積 四角形の面積を求める公式は、どれも三角形の面積を求める公式から得ることが出来ました円に内接する正方形を元の伸縮率にした四角形が最大面積を与えるということになりま すね。 S(H)さんが上記の問題を考察されました。(平成24年2月12日付け) 面積は、適当に座標をもうけ、四角形を2つに分け足すと、
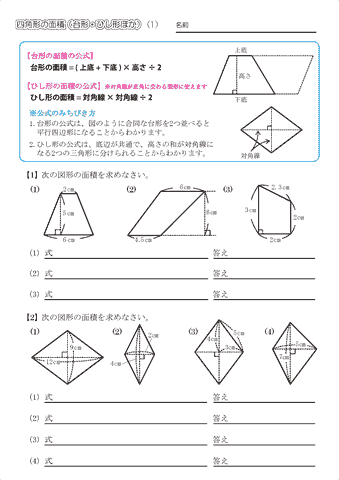



小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生
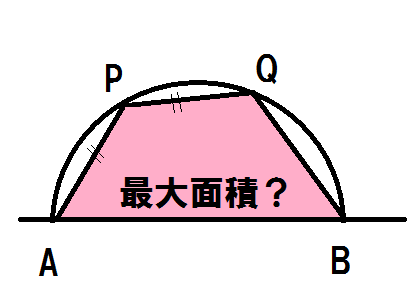



半円に内接するある四角形の最大の面積を求めるの問題 数学の星
問題 (正方形、長方形、平行四辺形、台形、ひし形、三角形、円を提示する) 面積の求め方が分かっている図形はどれでしょう。 四角形や三角形は求めることができます。 円はまだ学習していません。 これまでの面積の学習を生かして、円の面積の円 円 半円 扇形 円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 lc形 l形 c形 円形 パイプ 楕円 長穴 多角形 六角形 八角形 その他 円 円に内接する四角形 円に内接する四角形の性質は、高校数学の範囲ですが、中学生も知っておくと便利です。 それに、中学生が学習してもなんなく習得できます。簡単です。 例1 下の図で、角 \(x\) を求めなさい。 解答 円に




19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート




標準 三角比と円に内接する四角形 なかけんの数学ノート
極座標における円の方程式の一般形と例題 円に内接する四角形の面積を求める公式 正八面体の体積、表面積、外接球の半径、内接球の半径 正四面体の高さと体積の求め方 図形の面積を求める公式たち19個 円の面積を積分で計算する2通りの方法 楕円に本日のお題 四角形 \(\mbox{ABCD}\) が円に内接し \\mbox{AB}=2,\ \mbox{BC}=4,\ \mbox{CD}=4,\ \mbox{DA}=3\ であるとき,四角形 \(\mbox{ABCD ひし形(対角線直交四角形)の面積=対角線×対角線÷2 円周=直径×円周率(314)=半径×2×円周率(314) 円の面積=半径×半径×円周率(314) おうぎ形の弧の長さ=円周×中心角/360=直径×314×中心角/360




円に内接する四角形の面積 ブラーマグプタの公式 怜悧玲瓏 高校数学を天空から俯瞰する




面積の求め方 計算公式一覧
底面積の求め方は?5分でわかる計算、円柱、円錐、四角柱、三角柱の底面積 立方体の底面積 立方体は全ての辺が同じ長さです。よって底面の面積は「正方形の面積」を求めればよいですね。立方体の底面積は下記の通りです。 立方体の底面積=5×5=25cm 2入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 共学校 面積比 円 図形NOTE logix出版 角度 1日目 直角三角形 4年生 女子校 相似 立方体 長方形 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 ファイナル 二等辺切り口の円の半径をrとすれば、 であって、この範囲の1つのrの値に対して、(2)より、底面の四角形abcdの面積の最大値は ,球の中心oと四角形abcdとの距離は三平方の定理より です。これが、四角錐の高さになります。
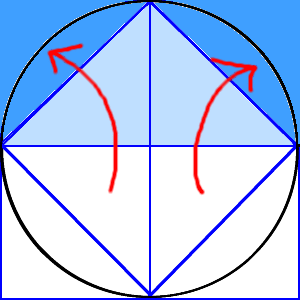



6年算数 円の面積 1 アニメでわかる教え方




有名問題 定理から学ぶ高校数学 A Twitter 1 27おすすめの問題 2倍角の公式 ブレートシュナイダーの公式 T Co Ulvofdfrkr 四角形の面積の公式として有名な ブレートシュナイダーの公式 を証明します 円に内接する四角形の面積を求める
$3$ 辺の長さと面積がすべて整数であるような三角形を「ヘロンの三角形」(Heronian triangle)と呼ぶ「ピタゴラスの三角形」(各辺の長さがすべて整数であるような直角三角形)は「ヘロンの三角形」であるよって, $1$ 組の辺の長さが等しい $2$ つの「ピタゴラスの三角形」の等辺を貼り合わせたり文献1によると,三角形,四角形,そして 円などの面積は,小学校で学習し,その値を 求める公式も知っている。小学校5年生の教 科書2によると,円の面積を求める公式を作 成するときに,次の2つの方法を扱っている。円に内接する四角形の面積(4辺から) 円に内接する四角形の面積(4辺から) 円に内接する四角形の4辺から四角形の面積と周囲の長さを計算します。 四角形の面積(4辺と対角の和から) 四角形の面積(4辺と対角の和から) 四角形の4辺と向かい合う1組の




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ




A8 A 70 Abcd Ab4 5 Cd7 Da10 See How To Solve It At Qanda
周長一定の三角形のうち、面積が最大になるのは正三角形である事を証明せよ。 問題2 与えられた円に外接する三角形で、面積が最小になるのは正三角形である事を証明せよ。 (ヒントはヘロンの公 平行四辺形の面積は、 「面積 底辺 高さ」 「 面 積 = 底 辺 × 高 さ 」 で求められます。 たとえば、「底辺 4 c m ,高さ 3 c m の平行四辺形」の面積は 4 × 3 = 12 c m 2 となります。 これは、平行四辺形の右端の直角三角形を切り取って左側に移すと 「たて 3 c m




高校数学 対角線の長さとなす角で表された四角形の面積公式 S 1 2pqsin8 裏技 の証明 対角線の長さの和が一定である四角形の面積の最大 受験の月



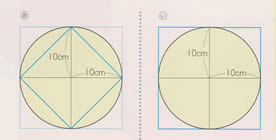
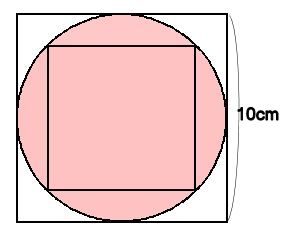
半径5cmの円の中に 下のような 正方形をかきました この正方形の 面積は何cmですか




三角比を使って円に内接する四角形の辺の長さ 面積を求める方法 数学i By Okボーイ マナペディア
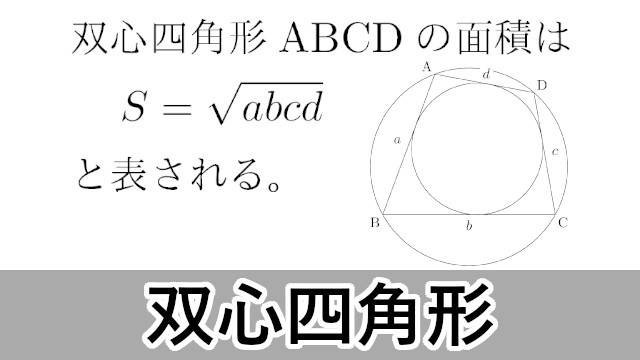



双心四角形の面積 外接円と内接円の両方をもつ四角形 大学入試数学の考え方と解法




高校数学 円に内接する四角形の計量 基本と裏技のまとめ トレミーの定理 ブラーマグプタの公式他 受験の月



ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典




高校数学 三角比 円に内接する四角形の面積求め方まとめと



円に内接する四角形の頻出問題 数学の雫



円の面積 1 5
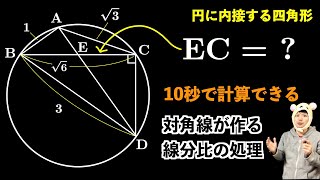



円に内接する四角形 対角線の線分比の処理 Youtube




高校数学 円に内接する四角形の対角線の長さと面積 受験の月



図形と計量 正弦定理 余弦定理 面積への応用について 日々是鍛錬 ひびこれたんれん



円に内接する四角形の面積 ブラーマグプタの公式 怜悧玲瓏 高校数学を天空から俯瞰する




標準 おうぎ形と正方形の面積 なかけんの数学ノート



円に内接する四角形abcdについて 対角線acの長さ 辺ad Yahoo 知恵袋
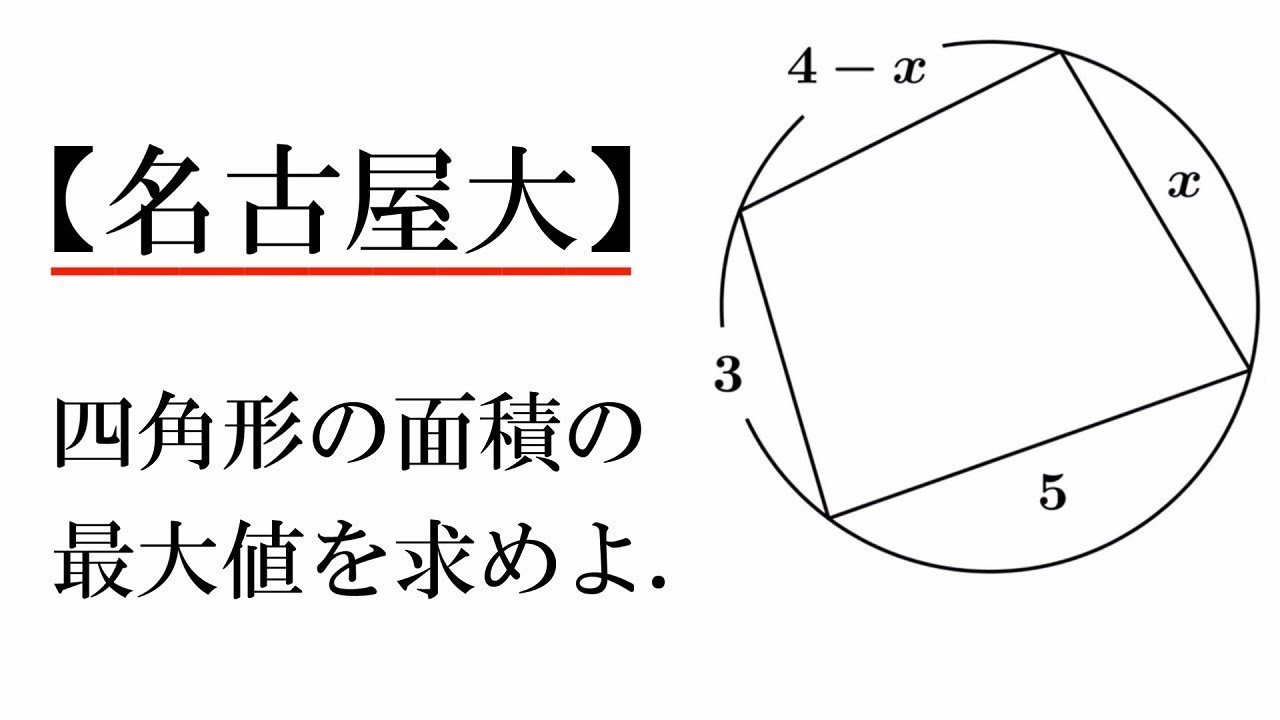



名古屋大 円に内接する四角形と三角比 超わかる 高校数学 A 演習 三角比 26 Youtube



七五三 三角形から円に内接する四角形へ




面積の求め方 計算公式一覧



円に内接する四角形の面積を求める公式 具体例で学ぶ数学



数学i Aチェック リピート 第4章 2図形への応用 5 円に内接する四角形 Pukiwiki



例題 円に内接する四角形 Youtube




円に内接する四角形の面積を求めるブラーマグブタの公式 2017年度前期日程の大阪教育大学教育学部入試問題 身勝手な主張




円に内接する四角形abcdにおいてab 2 4 Cd 3 Da 2とするとき Clear




5 0 Sqrt3 1 Abcd Ab1 B Descubre Como Resolverlo En Qanda




円に外接する四角形の重要な2つの性質 高校数学の美しい物語



Math 算数のコツ 18 円の中の正方形 働きアリ The 2nd




19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート




4辺が与えられたとき 面積最大になる四角形は 身勝手な主張




面積の求め方 算数の教え上手 学びの場 Com



四角形の種類と性質 面積の公式について 中学受験 ゲーム大好き息子の偏差値32からの挑戦



3



円の中の正方形



七五三 三角形から円に内接する四角形へ
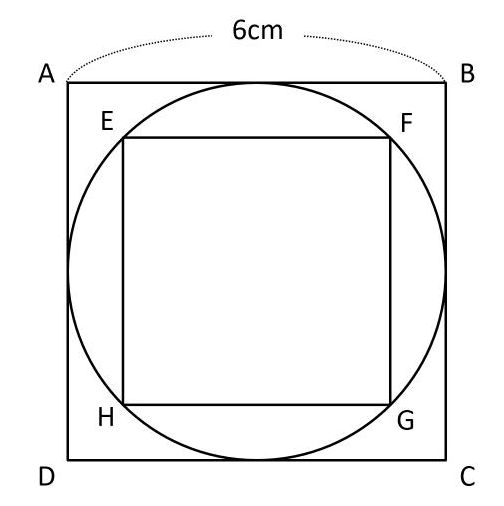



正方形の対角線の長さを求めたい 小学生が算数の知識を使ってどこまでできる 中学受験ナビ




面積が等しいならば 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog
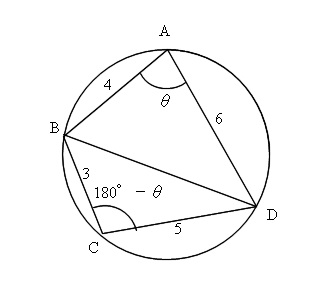



円に内接する四角形の面積の求め方と定理の使い方




円に内接する四角形の面積をサインを使って求める問題 数学i By ふぇるまー マナペディア



48s96ub7b0z5f Net Naisetsu Shikakukei




円に内接する四角形の面積 数学i 三角比 Youtube




図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト




7 Abcd A Descubre Como Resolverlo En Qanda




円に内接 外接する四角形の性質まとめ 数学の偏差値を上げて合格を目指す




正方形と円で囲まれた図形の面積 おわり Takapの数学日記
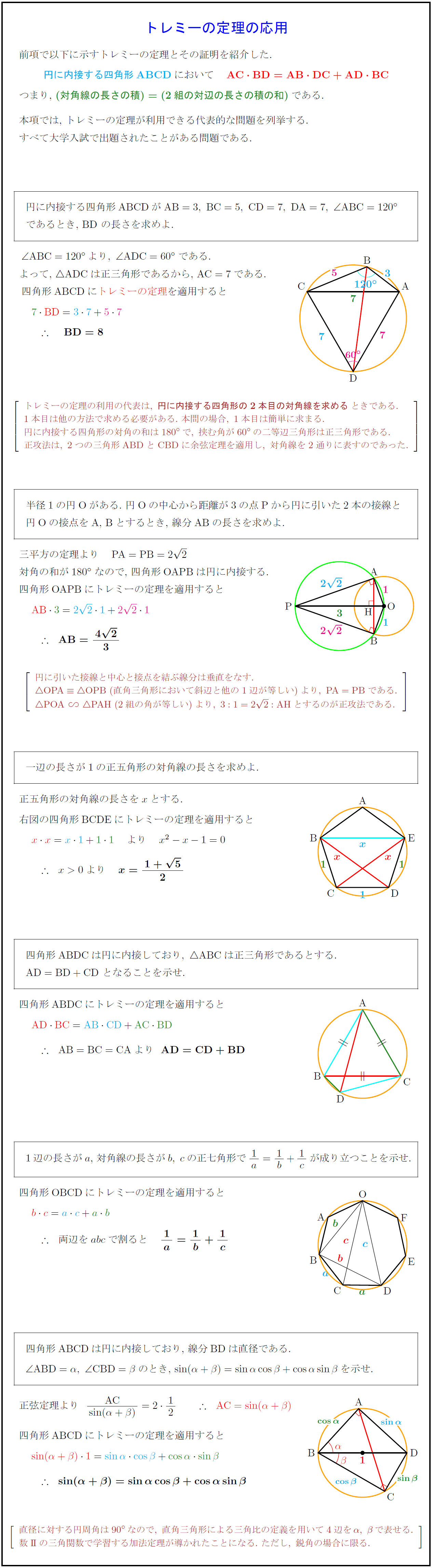



高校数学 トレミーの定理 裏技 の応用6種 円に内接する四角形の対角線の長さなど 受験の月




Edux 6正方形に内接する円




この場合の円に内接する四角形abcdの面積はどのようにして求めるのか教えてください Clear
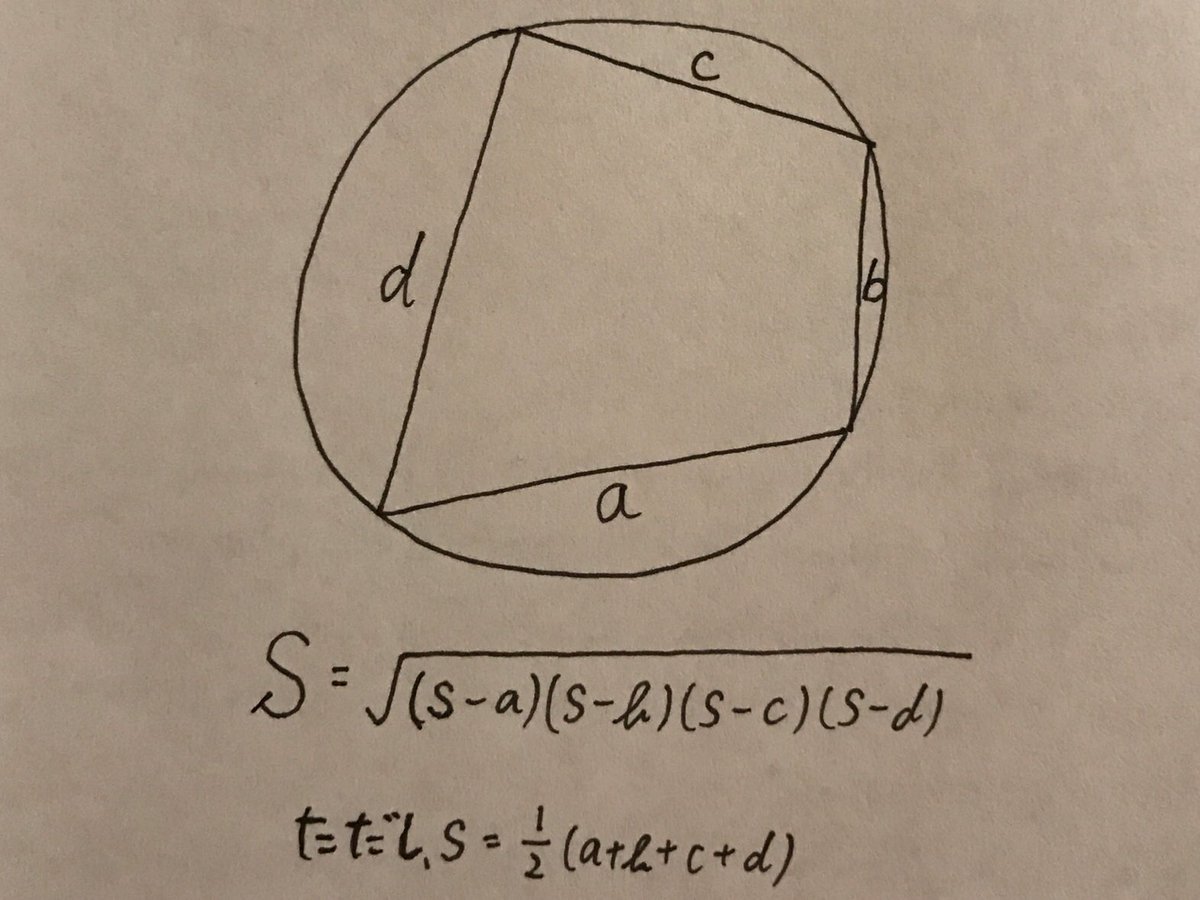



円に内接する四角形の面積sを求めてるなうに使っていいよ Twitter Search




Sin Abc0 Sinz Abcsqrt1 Descubre Como Resolverlo En Qanda



早大理工数学 09年 4



3
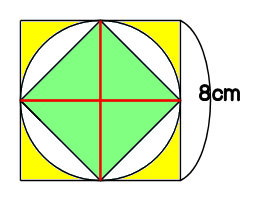



円の中の正方形 基礎




Mondai55
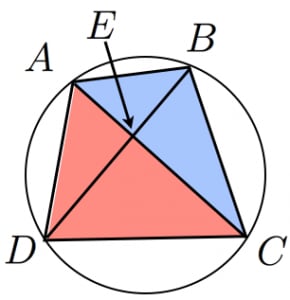



円に内接する四角形の性質とその証明まとめ 高校数学の美しい物語
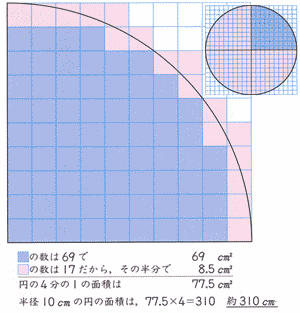



実践記録算数5年
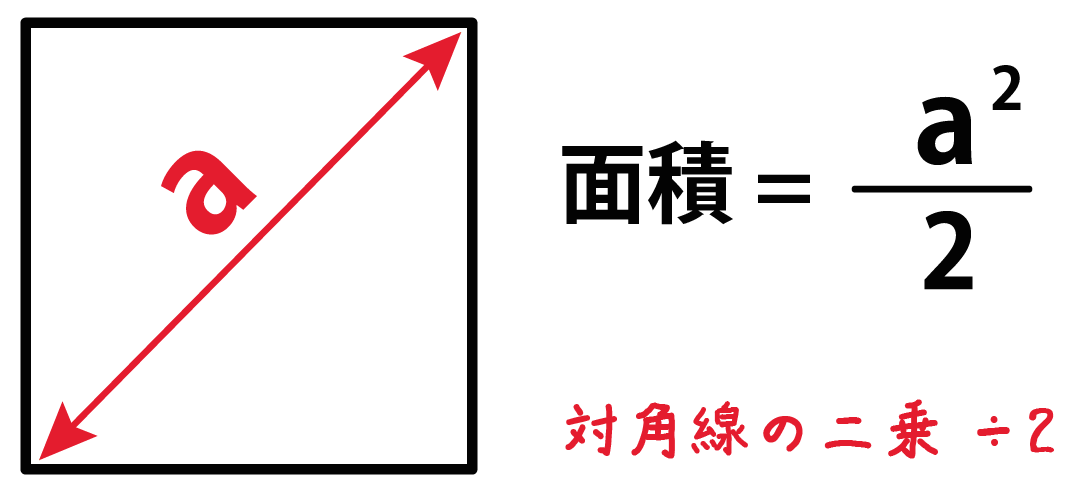



簡単公式 対角線で正方形の面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく




高校数学 円に内接する四角形の面積ブラーマグプタの公式 裏技 の証明と円に内接しない四角形の面積ブレートシュナイダーの公式 裏技 受験の月



Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau
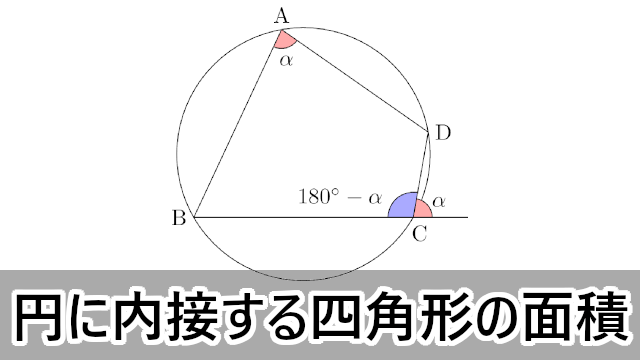



数学ia 円に内接する四角形の面積 大学入試数学の考え方と解法
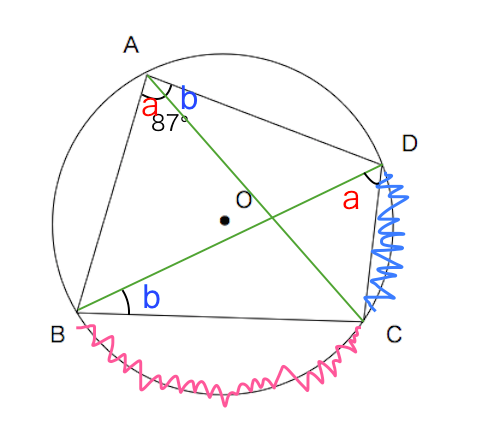



円に内接する四角形 苦手な数学を簡単に
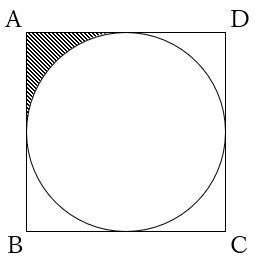



半径の分からない円の面積 中学受験プロ講師ブログ



2
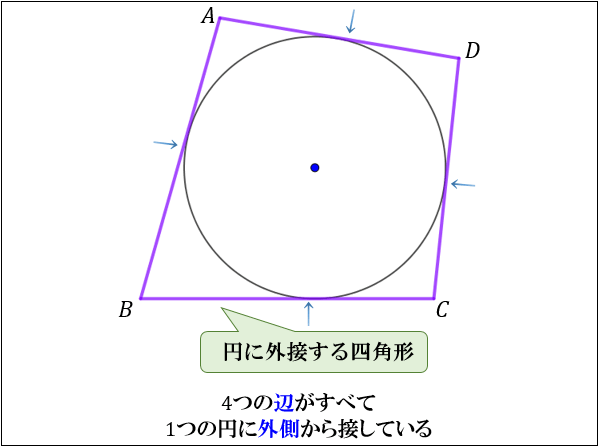



円に外接する四角形の性質まとめ 向かい合った辺の合計が等しくなる理由 アタリマエ



内接円とは 内接円の半径の公式や求め方 性質 書き方 受験辞典



算数の 図形から面積を求める問題に悩んでます 四角形abcdと四角 Yahoo 知恵袋
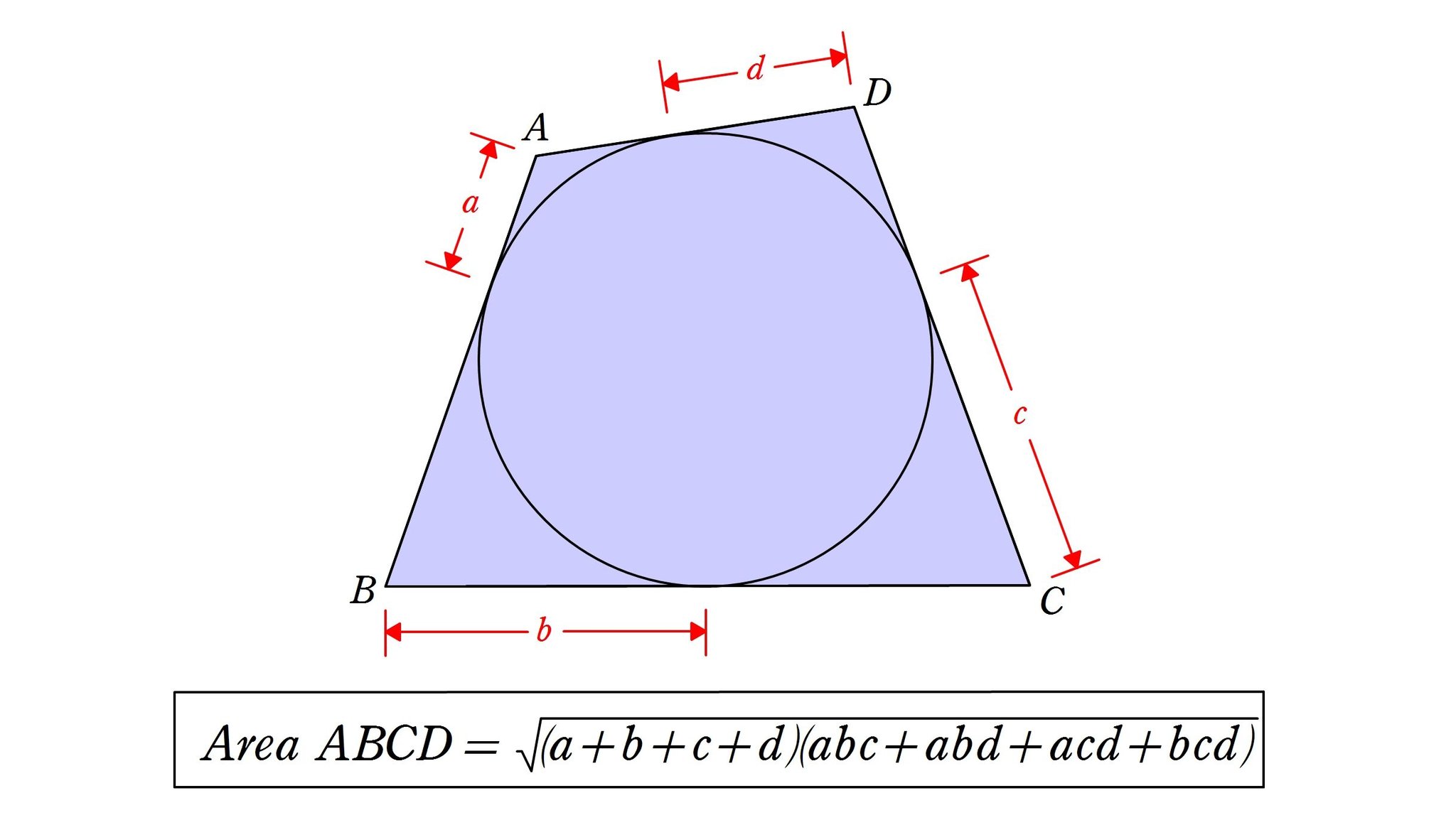



ポテト一郎 さんのツイート 円に外接する四角形の面積 なんと 角の大きさに依存しません




勉強しよう数学 円に内接する四角形の対角線の交差点までの長さ
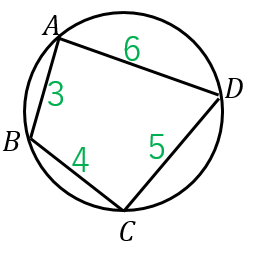



円に内接する四角形の面積を求める公式 具体例で学ぶ数学



円に内接する四角形abcdにおいて 2つの対角線ac の交点を Yahoo 知恵袋



1




円に内接する四角形の性質 中学数学の無料オンライン学習サイトchu Su




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく



入試問題に挑戦第61回




高校数学 数 96 円に内接する四角形 Youtube




円の面積 算数用語集




円に内接している四角形の面積の最大値について Okwave



ファイル Bous2 Jpg Wikipedia




数1の円に内接する四角形の問題です よろしくお願いします Clear



面積の求め方 算数の教え上手 学びの場 Com



円の中の正方形




円に内接する四角形 小学5年への説明 再掲 Okwave
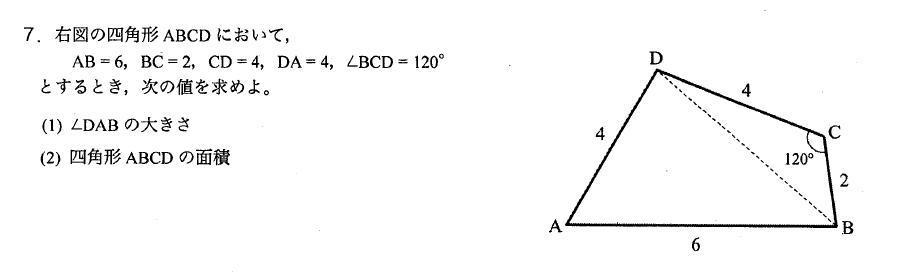



角度 四角形の面積を求める問題です 大学入試数学問題の解説 解答




円に内接する四角形の面積を四辺の長さで表す 2019年度前期日程の京都府立大学生命環境学部の入試 身勝手な主張




19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート
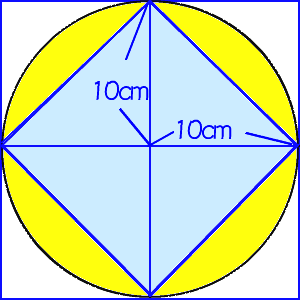



6年算数 円の面積 1 アニメでわかる教え方




ポテト一郎 Sur Twitter 円に外接する四角形の面積比




円に内接する四角形の性質 高校数学の知識庫




ブラーマグプタの公式 17年 大阪教育大 数学日和
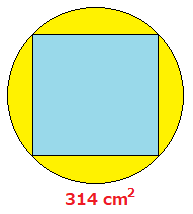



円と四角形の面積 の解答と解説 多目的ルーム 楽天ブログ




ブラーマグプタの公式 円に内接する四角形の面積 大学入試数学の考え方と解法
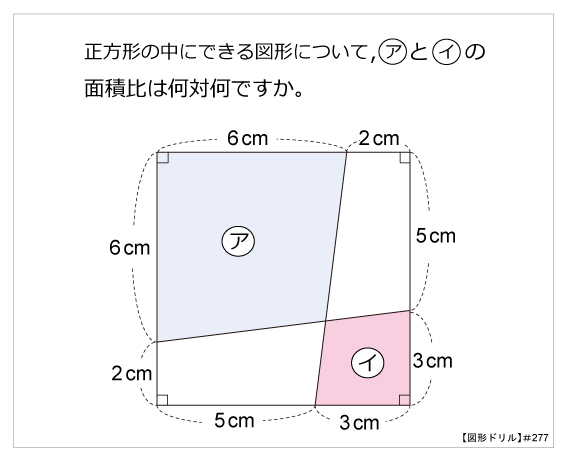



図形ドリル 第277問 2つの四角形の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦
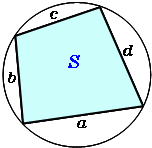



円に内接する四角形の面積 4辺から 高精度計算サイト



Http Www Edu Town Sera Hiroshima Jp Seranishi Es Sidouann Sidouannsyuu Ryoutosokutei 6nennennnomennseki Pdf



0 件のコメント:
コメントを投稿